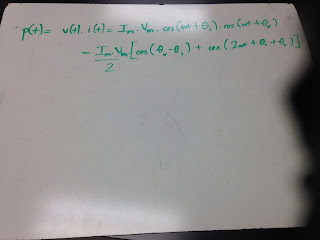Part 1: Op Amp Circuits
Today, we discuss about the op amp in the ac circuits and oscillators. We also did a experiment about to create an oscillators.
First, to dealt with the op amp ac circuit, we need to remember two important properties of an ideal op amp: 1. No current enters either of its input terminals, 2. The voltage across its input terminals is zero.
We did a practice with an op amp in the ac circuit.
Oscillators.
An oscillator is a circuit that produces an ac waveform as output when powered by a dc input.
In order for sine wave oscillators to sustain oscillations, they must meet the Barkhausen criteria:
1. The overall gain of the oscillator must be unity or greater. Therefore, losses must be compensated for by an amplifying device.
2. The overall phase shift (from input to output and back to the input) must be zero.
The Wien-bridge oscillator
feedback ratio is (V2/V0) = Zp/(Zp+Zs),
which Zs= R1+Zc1, Zp = R2//Zc2.
Based on the 2nd Barkhausen criterion, V2 must be in phase with Vo, which implies that the feedback ratio is purely real, the imaginary part must be zero. Then we deduce the ratio with the assumption R1=R2=R, and C1=C2=C, the feedback ratio is 1/3.
Based on the 1st Barkhausen criterion, the op amp must compensate by providing a gain of 3 or greater so that the overall gain is unity or greater than 1.
Vo/V2 = 1 + Rf/Rg = 3 => Rf = 2Rg
Part 2: The Op Amp Relaxation Oscillator Lab
Purpose: The lab aims to create an op amp relaxation oscillator with desired frequency.
Theory and Pre-lab
This is an op amp relaxation oscillator.
It operates as the following process. Let’s consider
that the voltage Vplus is larger than voltage Vminus . The voltage on the non-inverting input of the
OP AMP is larger than the voltage on the inverting input. The OP AMP will try to amplify the
difference between the input voltages with a very large non-inverting voltage gain, causing the
OP AMP output voltage to saturate at the positive supply voltage VCC (+ 15 Volts).
When the situation is reversed and voltage Vminus is larger than voltage Vplus , the voltage
on the inverting input of the OP AMP is larger than the voltage on the non-inverting input. The
OP AMP will try to amplify the difference between the input voltages but now with a very large
inverting voltage gain, and the OP AMP output voltage saturates at the negative power supply
voltage VEE (-15 Volts).
The period of oscillation is given by the expression
T = 2RC ln {(1+B)/ (1-B)} seconds, B=R1/(R1+R2).
Our desired frequency is 158Hz. Based on the above formula, we calculate the resistor required R is 2880 Ohm provided R1 = R2 = 1kOhm.
The period is T=1/f = 6.329ms
The set-up for the relaxation op amp oscillator.
The oscillators has the period meets with our calculations: periods is about 6ms.
The measured values match with the desired value, percent error is 4%.
Part 3: Instantaneous and average power
This shows us that the instantaneous power has two parts. The first part is constant or time
independent. Its value depends on the phase difference between the voltage and the current.
The second part is a sinusoidal function whose frequency is 2ω, which is twice the angular frequency of the voltage or current.
the graph of the instantaneous current, voltage, and power. The period of the instantaneous power is half of the instantaneous current and voltage.
The average power
Define:
The average power is the average of the instantaneous power over one period
After substituting the p(t), the average power is
In two special case,
1. when the current and voltage are in phase θ v = θ i, the circuit is purely resistive, P = ½ V m I m = ½ I2
mR = ½ | I | 2 R
2. When θ v − θ i = ± 90, the circuit is purely reactive. P = ½ V m I m cos (90) = 0.
Conclude: A resistive load (R) absorbs power at all times, while a reactive load (L or C)
absorbs zero average power.
We did a practice to calculate the power of each element in the above circuit. We convert the circuit into frequency domain, then find the currents in each elements, then find the average power of each element.
Maximum average power transfer
After analyzing the Thevenin equivalent of the circuit with the load impedance.
ZL = Rl +jXL,
Zth = Rth +jXth
We conclude,
For maximum average power transfer, the load impedance ZL must be equal to the
complex conjugate of the Thevenin impedance ZTh.
ZL = Rth - jXth.
then the maximum average power is P = (Vth^2)/(8Rth)
We do a practice to find the Zl to gain the maximum average power for this circuit. First, we find the thevenin impedance by short circuit the independent voltage source and open circuit the independent current circuit. Second, the conjugate of the Thevenin impedance is the load impedance gaining maximum average power.
Conclusion:
Today, we discuss more about the AC source circuit. We practice to analyze the AC circuit including an op amp. We also study about the oscillators and make a relaxation op amp oscillator with the given frequency. We did the experiment successfully with the agreement between the measured value and the given value. Additionally, we discuss about the instantaneous power and the average power P = 1/2 * Vm*Im*cos(θ v − θ i) which is independent from time. We also deduce the thevinen equivalent to find the load impedance Zl = Rth -jXth gaining maximum average power. Pmax = (Vth^2)/(8*Rth)