Sunday, February 28, 2016

DAY 1: MATLAB

INTRODUCTION TO NUMERICAL COMPUTATION

USING MATLAB AS A CALCULATOR
6+3/2
ans =
    7.5000
>> 3+4
ans =
     7
>> (6+3)/2
ans =
    4.5000
>> 11^2
ans =
   121
>> 2*3+4^3
ans =
70

MATH FUNCTIONS
3=4
 3=4
  |Error: The expression to the left of the equals sign is not a valid target for an assignment.
 >> 3+4
ans =
     7
ASSIGNING EXPRESSIONS TO VARIABLES
x=2*5
x =
    10
>> x
x =
    10
>> x=2*5;
>> x
x =
    10

CREATING AN ARRAY
            CREATING A ROW VECTOR
>> X= [2 4 5 6 7]
X =
     2     4     5     6     7
            CREATING A COLUMN VECTOR
Y=[3;5;3;5;6]
Y =
     3
     5
     3
     5
     6
            CREATING A MATRIX
XY=[1 1 1 1;2 2 2 2;3 3]
Error using vertcat
Dimensions of matrices being concatenated are not consistent.
 >> XY=[1 1 1 1;2 2 2 2;3 3 3 3]
XY =

     1     1     1     1
     2     2     2     2
     3     3     3     3

1.        C=[1 2 3;4 5 6;7 8 9]
C =
     1     2     3
     4     5     6
     7     8     9

AUTOMATICALLY CREATING VECTORS
Using the Colon
R=0:0.5:10
R =
  Columns 1 through 11
         0    0.5000    1.0000    1.5000    2.0000    2.5000    3.0000    3.5000    4.0000    4.5000    5.0000
  Columns 12 through 21
    5.5000    6.0000    6.5000    7.0000    7.5000    8.0000    8.5000    9.0000    9.5000   10.0000
TRANSPOSING ARRAYS
test1=[2 3 4 5]
test1 =
     2     3     4     5
>> tes2=test1'
tes2 =
     2
     3
     4
     5

>> xx=[1 1;2 2;3 3]
xx =
     1     1
     2     2
     3     3
>> xx=xx'
xx =
     1     2     3
     1     2     3

APPLYING FUNCTIONS TO ROW VECTORS
x=[0:pi/10:2*pi]
x =
  Columns 1 through 11
         0    0.3142    0.6283    0.9425    1.2566    1.5708    1.8850    2.1991    2.5133    2.8274    3.1416
  Columns 12 through 21
    3.4558    3.7699    4.0841    4.3982    4.7124    5.0265    5.3407    5.6549    5.9690    6.2832
y =
  Columns 1 through 11
         0    0.3090    0.5878    0.8090    0.9511    1.0000    0.9511    0.8090    0.5878    0.3090    0.0000
  Columns 12 through 21
   -0.3090   -0.5878   -0.8090   -0.9511   -1.0000   -0.9511   -0.8090   -0.5878   -0.3090   -0.0000
>> z=cos(x)
The results make sense.
z =
  Columns 1 through 11
    1.0000    0.9511    0.8090    0.5878    0.3090    0.0000   -0.3090   -0.5878   -0.8090   -0.9511   -1.0000
  Columns 12 through 21
   -0.9511   -0.8090   -0.5878   -0.3090   -0.0000    0.3090    0.5878    0.8090    0.9511    1.0000
>> g=exp(x)
g =
  Columns 1 through 11
    1.0000    1.3691    1.8745    2.5663    3.5136    4.8105    6.5861    9.0170   12.3453   16.9020   23.1407
  Columns 12 through 21
   31.6821   43.3762   59.3867   81.3068  111.3178  152.4060  208.6603  285.6784  391.1245  535.4917
>> h=log10(x)
h =
  Columns 1 through 11
      -Inf   -0.5029   -0.2018   -0.0257    0.0992    0.1961    0.2753    0.3422    0.4002    0.4514    0.4971
  Columns 12 through 21
    0.5385    0.5763    0.6111    0.6433    0.6732    0.7013    0.7276    0.7524    0.7759    0.7982
ARRAY OPERATIONS
BB=cos(x)-sin(x)
BB =
  Columns 1 through 11
    1.0000    0.6420    0.2212   -0.2212   -0.6420   -1.0000   -1.2601   -1.3968   -1.3968   -1.2601   -1.0000
  Columns 12 through 21
   -0.6420   -0.2212    0.2212    0.6420    1.0000    1.2601    1.3968    1.3968    1.2601    1.0000
=> MAKE SENSE
>> CC=cos(x)*sin(x)
Error using  *
Inner matrix dimensions must agree.
 >> DD=cos(x).*sin(x)
DD =
  Columns 1 through 11
         0    0.2939    0.4755    0.4755    0.2939    0.0000   -0.2939   -0.4755   -0.4755   -0.2939   -0.0000
  Columns 12 through 21
    0.2939    0.4755    0.4755    0.2939    0.0000   -0.2939   -0.4755   -0.4755   -0.2939   -0.0000
=> MAKE SENSE
ADDRESSING ARRAYS
            ADDRESSING SINGLE DIMENSIONAL ARRAYS
            ADDRESSING MATRICES
>> xy=[1 2 3;4 5 6;7 8 9]
xy =
     1     2     3
     4     5     6
     7     8     9
>> xy(1,1)
ans =
     1
>> xy(1,:)
ans =
     1     2     3
>> xy(:,1)
ans =
     1
     4
     7
>> xy(1:2,:)
ans =
     1     2     3
     4     5     6
>> xy(:,2:3)
ans =
     2     3
     5     6
     8     9
CREATING SIMPLE PLOTS
CREATIG A 2-D PLOT WITHOUT STYLE OPTIONS
degree=0:2*pi/100:2*pi;
>> output=sin(degree);
>> plot(degree,output)

                                   ADDING ADDITIONAL PLOTS TO THE SAME GRAPHS
degree=0:2*pi/100:2*pi;
>> output=sin(degree);
>> plot(degree,output)
>> hold off
>> degree=0:2*pi/100:2*pi;
>> output=sin(degree);
>> plot(degree,output)
>> hold on
>> degree1=0:2*pi/100:2*pi;
>> output1=cos(degree);
>> plot(degree1,output1)
hold off
>> degree=0:2*pi/100:2*pi;
>> output=sin(degree);
>> plot(degree,output)
Plot(degree,sin(degree),degree,cos(degree))

SCRIPT FILES
As to run script need to address the script location to matllab, or save it to matlab.
script
%test script square
square=a^2;
squareroot=sqrt(a);

command window
>> a=4;
>> mt;
>> square
square =
    16
>> squareroot
squareroot =

     2

SOLVING SIMULTANEOUS EQUATIONS
ASSIGNMENT 1:
>> r=[1 -1 -1;20 0 10;0 5 -10]
r =
     1    -1    -1
    20     0    10
     0     5   -10
>> v=[0;15;7]

v =
     0
    15
     7
>> i=inv(r)*v
i =
    0.8429
    1.0286
   -0.1857
=> R3= -0.1857
PLOTING EXPONETIALS
>> plot(t,x1,t,x2,t,x3)
>> tau1=1;
>> tau2=tau1*0.5;
>> tau3=tau1*2;
>> x1=5*exp(-t/tau1);
>> x2=5*exp(-t/tau2);
>> x3=5*exp(-t/tau3);
>> plot(t,x1,t,x2,t,x3)
 
ADDING SINUSOIDS
ASSIGNMENT 1
1. >> t=linspace(0,500);
>> ca=2*(exp(-t/100));
>> cb=2*(exp(-t/200));
>> plot(t,ca)
>> plot(t,cb)

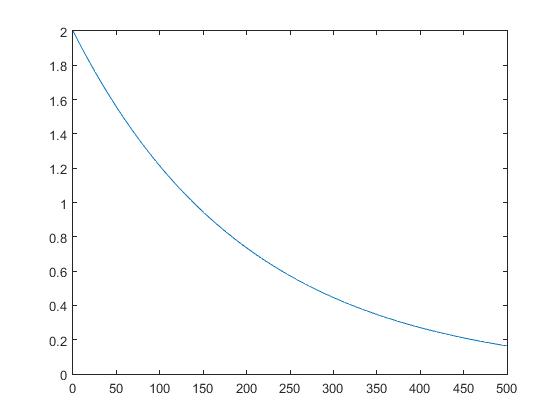
>> plot(t,ca,t,cb)

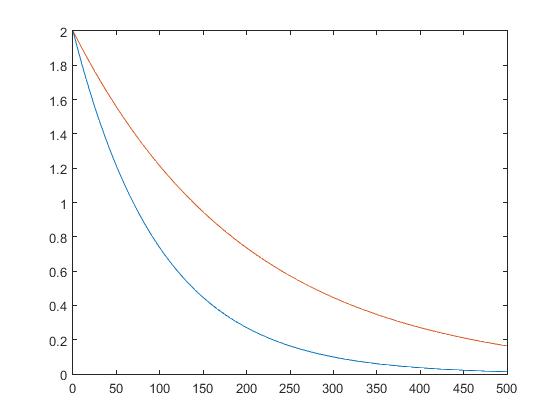
ca will have the lowest output sooner.
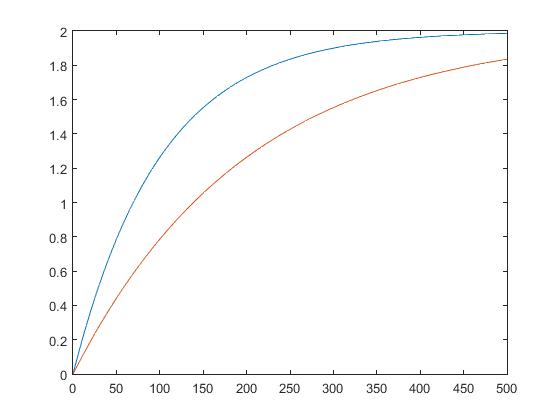
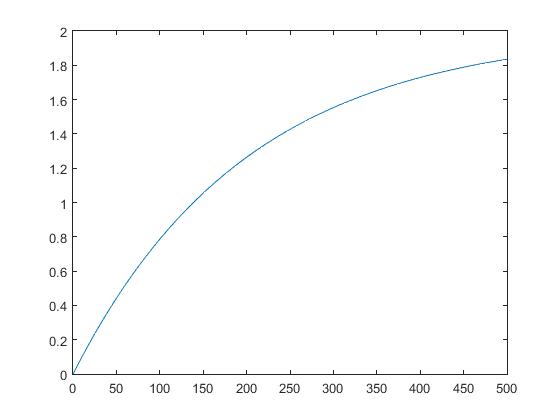
>> ca2=2*(1-exp(-t/100));
>> cb2=2*(1-exp(-t/200));
>> plot(t,ca2,t,cb2)

>> plot(t,ca2)

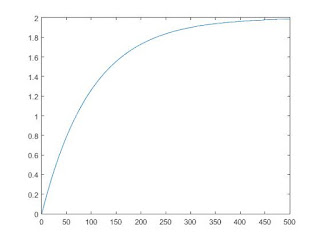
>> plot(t,cb2)



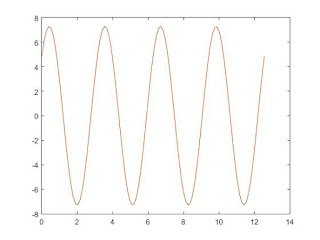
2, Assignment 2

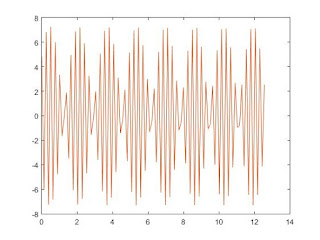
t=linspace(0,4*pi);
>> theo=7.29*sin(2*t+0.727);
>> mat=3*sin(2*t+10*pi/180)+5*cos(2*t-30*pi/180);
>> plot(t,theo,t,mat);

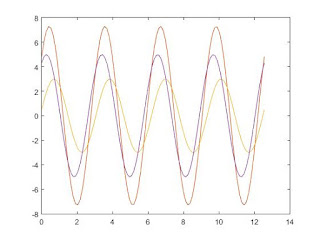
>> mat1=3*sin(2*t+10*pi/180);
>> mat2=5*cos(2*t-30*pi/180);
>> plot(t,theo,t,mat,t,mat1,t,mat2)

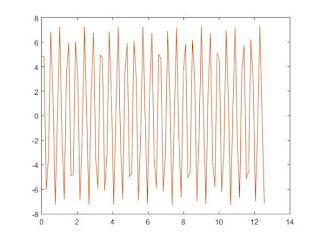
2.
f=10;
>> w=2*pi*f;
>> theo=7.29*sin(w*t+0.727);
>> mat=3*sin(w*t+10*pi/180)+5*cos(w*t-30*pi/180);
>> plot(t,theo,t,mat);

A Script to implement this with any f(HZ)
>> w=2*pi*f;
>> theo=7.29*sin(w*t+0.727);
>> mat=3*sin(w*t+10*pi/180)+5*cos(w*t-30*pi/180);
>> plot(t,theo,t,mat);

f=20;
>> assi

COMPLEX NUMBER
OPERATIONS WITH COMPLEX NUMBERS
>> A=2+2j, B=-1+3j, C=2+j
A =
   2.0000 + 2.0000i
B =
  -1.0000 + 3.0000i
C =
   2.0000 + 1.0000i
>> D=(A*B)/C
D =
  -2.4000 + 3.2000i
>> E=(A+B)*C
E =
  -3.0000 +11.0000i
FUNCTIONS TO CONVERT FROM RECTANGULAR TO POLAR
EXERCISE 1:
>> A=3+4j; B=3-2j; C=2*exp(50*pi/180*j);
>> D=(A+C)/B
D =
   0.1379 + 1.9360i
EXERCISE 2:
>> E
E =
  -3.0000 +11.0000i
>> abs(E)
ans =
   11.4018
>> angle(E)
ans =
    1.8370
>> angle(E)*180/pi
ans =
  105.2551

ASSIGNMENT
>> A1=3+2j; A2=-1+4j; B=2-2j
B =
   2.0000 - 2.0000i
>> A1=3+2j; A2=-1+4j; B=2-2j;
>> C=(A1*B)/A2
C =
  -1.0588 - 2.2353i
2.
>> angle(A1)*180/pi, abs(A1)
ans =
   33.6901
ans =
    3.6056

>> %3.6056<33.6901
>> angle(A2)*180/pi, abs(A2)
ans =
  104.0362
ans =
    4.1231
>>%4.1<104
>> 4<104
ans =
     1
>> angle(B)*180/pi, abs(B)
ans =
   -45
ans =
    2.8284
>> %2.8<-45
3.
>> D=(A1+B)*A2
D =
  -5.0000 +20.0000i
4.
>> T=[8+8j 2j;2j 4-4j]
>> P=[50j;-30j]
>> I=inv(T)*P
I =
   2.0588 + 2.9412i
   5.0000 - 3.5294i
>> I2=5-3.5294j; angle(I2)*180/pi, abs(I2)
ans =
  -35.2175
ans =
    6.1202
SOLVING FOR ROOTS OF EQUATIONS
EXERCISE 1
>> p=[1 4 3];
>> r=roots(p)
r =
    -3
-1
Assignment
1. >> p1=[1 1 4];
>> p2=[1 3 0 3];
>> p3=[1 3 4 2 7];
>> r1=roots(p1)

r1 =
  -0.5000 + 1.9365i
  -0.5000 - 1.9365i
>> r2=roots(p2)
r2 =

  -3.2790 + 0.0000i
   0.1395 + 0.9463i
   0.1395 - 0.9463i
>> r3=roots(p3)
r3 =
  -1.8222 + 1.2680i
  -1.8222 - 1.2680i
   0.3222 + 1.1474i
   0.3222 - 1.1474i


2.
>> p=[1 5 7 3];
>> s=roots(p)
s =
  -3.0000 + 0.0000i
  -1.0000 + 0.0000i
  -1.0000 - 0.0000i


>>  T=[1 1 0;2 4 1;1 3 3];
>> I=[0;1;7];
>> K=inv(T)*I

K =

     1
    -1
     3
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)